Probability Distributions

Overview

The distributions package provides a framework and implementations for some commonly used probability distributions. Continuous univariate distributions are represented by implementations of the RealDistribution interface. Discrete distributions implement IntegerDistribution (values must be mapped to integers) and there is an EnumeratedDistribution class representing discrete distributions with a finite, enumerated set of values. Finally, multivariate real-valued distributions can be represented via the MultivariateRealDistribution interface.

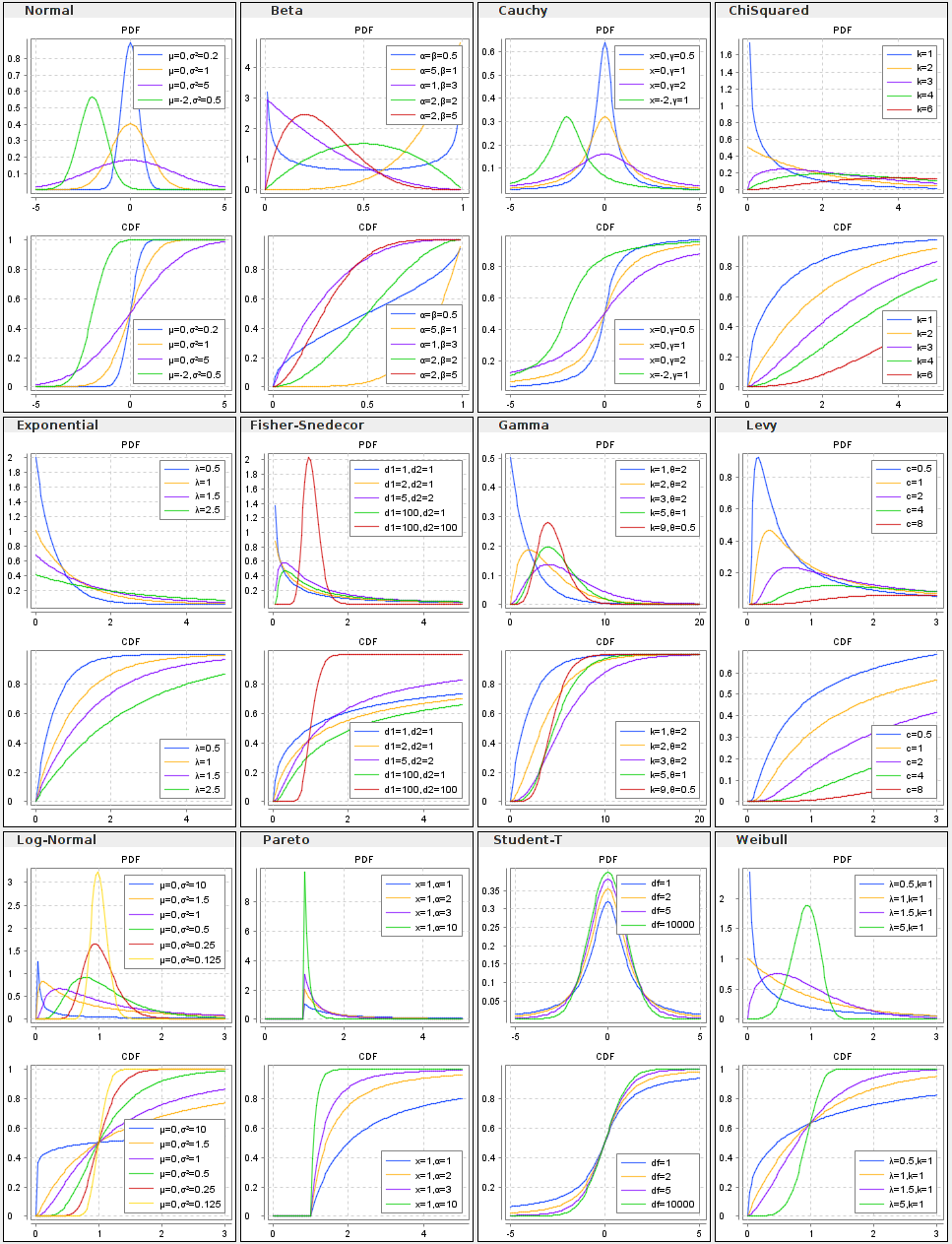
An overview of available continuous distributions:

Distribution Framework

The distribution framework provides the means to compute probability density functions (density(...)), probability mass functions (probability(...)) and distribution functions (cumulativeProbability(...)) for both discrete (integer-valued) and continuous probability distributions. The framework also allows for the computation of inverse cumulative probabilities.

For an instance f of a distribution F, and a domain value, x, f.cumulativeProbability(x) computes P(X <= x) where X is a random variable distributed as f, i.e., f.cumulativeProbability(...) represents the distribution function of f. If f is continuous, (implementing the RealDistribution interface) the probability density function of f is represented by f.density(...). For discrete f (implementing IntegerDistribution), the probability mass function is represented by f.probability(...). Continuous distributions also implement probability(...) with the same definition (f.probability(x) represents P(X = x) where X is distributed as f), though in the continuous case, this will usually be identically 0.

TDistribution t = new TDistribution(29);
double lowerTail = t.cumulativeProbability(-2.656);     // P(T(29) <= -2.656)
double upperTail = 1.0 - t.cumulativeProbability(2.75); // P(T(29) >= 2.75)

Inverse distribution functions can be computed using the inverseCumulativeProbability methods. For continuous f and p a probability, f.inverseCumulativeProbability(p) returns

• inf{x in R | P(X≤x) ≥ p} for 0 < p < 1,
• inf{x in R | P(X≤x) > 0} for p = 0.

For discrete f, the definition is the same, with Z (the integers) in place of R. Note that in the discrete case, the ≥ in the definition can make a difference when p is an attained value of the distribution.

User Defined Distributions

User-defined distributions can be implemented using RealDistribution, IntegerDistribution and MultivariateRealDistribution interfaces serve as base types.

These serve as the basis for all the distributions directly supported by Hipparchus. To aid in implementing distributions, the AbstractRealDistribution, AbstractIntegerDistribution and AbstractMultivariateRealDistribution provide implementation building blocks and offer basic distribution functionality. By extending these abstract classes directly, much of the repetitive distribution implementation is already developed and should save time and effort in developing user-defined distributions.